A demo of Experiment Manager

In this example, we use the ExperimentManager.

First, we initialize a grid world environment with finite state space and actions. A grid world is a simple environment with finite states and actions, on which we can test simple algorithms. The reward function can be accessed by: env.R[state, action], while the transitions by: env.P[state, action, next_state].

Then, we implement a value iteration algorithm for the action values:

\[Q(s, a) \leftarrow \sum_{s^{\prime}} p(s'|a, s)\left( R(s, a)+\gamma \max _{a^{\prime}} Q(s^{\prime}, a^{\prime}) \right).\]

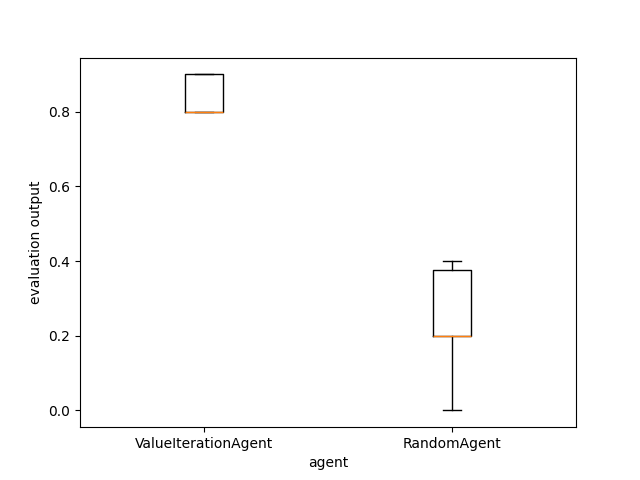
Finally, we compare with a baseline provided by a random policy using the ExperimentManager class which trains, evaluates and gathers statistics about the two agents.

[INFO] 08:47: ... trained!
[INFO] 08:47: Saved ExperimentManager(ValueIterationAgent) using pickle.
[INFO] 08:47: The ExperimentManager was saved in : 'rlberry_data/temp/manager_data/ValueIterationAgent_2024-10-25_08-47-28_4797ac29/manager_obj.pickle'
[INFO] 08:47: Running ExperimentManager fit() for RandomAgent with n_fit = 1 and max_workers = None.
[INFO] 08:47: ... trained!
[INFO] 08:47: Saved ExperimentManager(RandomAgent) using pickle.
[INFO] 08:47: The ExperimentManager was saved in : 'rlberry_data/temp/manager_data/RandomAgent_2024-10-25_08-47-29_2aff9cce/manager_obj.pickle'
[INFO] 08:47: Evaluating ValueIterationAgent...
[INFO] 08:47: Computing 10 evaluations.
[INFO] Evaluation:..........  Evaluation finished
[INFO] 08:47: Evaluating RandomAgent...
[INFO] 08:47: Computing 10 evaluations.
[INFO] Evaluation:..........  Evaluation finished

from rlberry_research.envs import GridWorld

# Create a grid world environment and an agent with a value iteration policy
env_ctor = GridWorld
env_kwargs = dict(
    nrows=3,
    ncols=10,
    reward_at={(1, 1): 0.1, (2, 9): 1.0},
    walls=((1, 4), (2, 4), (1, 5)),
    success_probability=0.9,
)
env = env_ctor(**env_kwargs)

import numpy as np
from rlberry.agents import AgentWithSimplePolicy


class ValueIterationAgent(AgentWithSimplePolicy):
    name = "ValueIterationAgent"

    def __init__(
        self, env, gamma=0.99, epsilon=1e-5, **kwargs
    ):  # it's important to put **kwargs to ensure compatibility with the base class
        """
        gamma: discount factor
        episilon: precision of value iteration
        """
        AgentWithSimplePolicy.__init__(
            self, env, **kwargs
        )  # self.env is initialized in the base class

        self.gamma = gamma
        self.epsilon = epsilon
        self.Q = None  # Q function to be computed in fit()

    def fit(self, budget=None, **kwargs):
        """
        Run value iteration.
        """
        S, A = env.observation_space.n, env.action_space.n
        Q = np.zeros((S, A))
        V = np.zeros(S)

        while True:
            TQ = np.zeros((S, A))
            for ss in range(S):
                for aa in range(A):
                    TQ[ss, aa] = env.R[ss, aa] + self.gamma * env.P[ss, aa, :].dot(V)
            V = TQ.max(axis=1)

            if np.abs(TQ - Q).max() < self.epsilon:
                break
            Q = TQ
        self.Q = Q

    def policy(self, observation):
        return self.Q[observation, :].argmax()

    @classmethod
    def sample_parameters(cls, trial):
        """
        Sample hyperparameters for hyperparam optimization using Optuna (https://optuna.org/)
        """
        gamma = trial.suggest_categorical("gamma", [0.1, 0.25, 0.5, 0.75, 0.99])
        return {"gamma": gamma}


# Create random agent as a baseline
class RandomAgent(AgentWithSimplePolicy):
    name = "RandomAgent"

    def __init__(self, env, **kwargs):
        AgentWithSimplePolicy.__init__(self, env, **kwargs)

    def fit(self, budget=None, **kwargs):
        pass

    def policy(self, observation):
        return self.env.action_space.sample()


from rlberry.manager import ExperimentManager, evaluate_agents

# Define parameters
vi_params = {"gamma": 0.1, "epsilon": 1e-3}

# Create ExperimentManager to fit 4 agents using 1 job
vi_stats = ExperimentManager(
    ValueIterationAgent,
    (env_ctor, env_kwargs),
    fit_budget=0,
    eval_kwargs=dict(eval_horizon=20),
    init_kwargs=vi_params,
    n_fit=4,
)
vi_stats.fit()

# Create ExperimentManager for baseline
baseline_stats = ExperimentManager(
    RandomAgent,
    (env_ctor, env_kwargs),
    fit_budget=0,
    eval_kwargs=dict(eval_horizon=20),
    n_fit=1,
)
baseline_stats.fit()

# Compare policies using 10 Monte Carlo simulations
output = evaluate_agents([vi_stats, baseline_stats], n_simulations=10)